Multivariate linear regression
Linear regression with multiple variables is also known as “multivariate linear regression”.
Notation
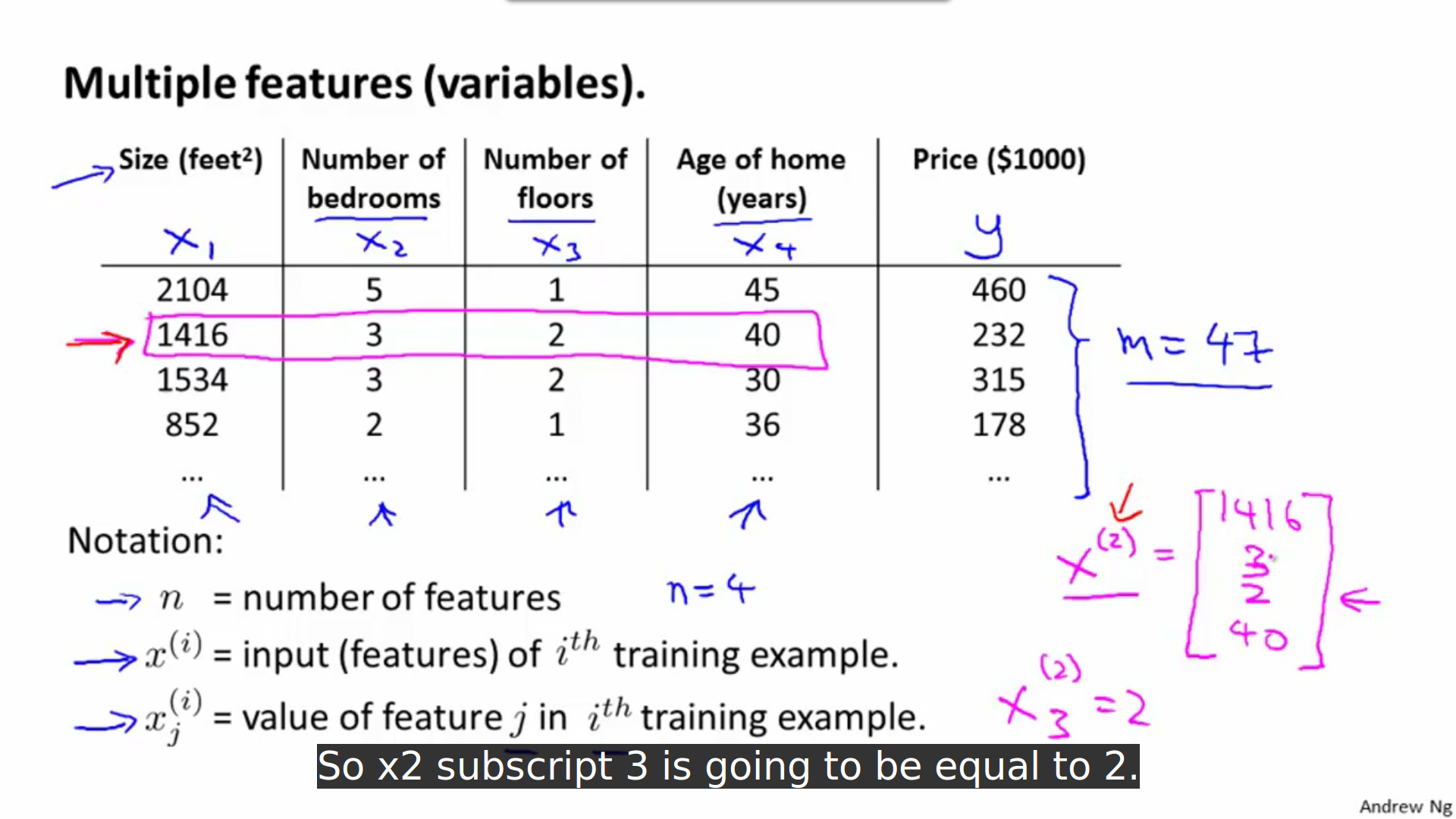
Hypothesis

Gradient descent
Formula:

Partial derivation will be like this:

Feature scaling
If scale of features differ widely, it may take long time to converge. So it is necessary to scale the feature.
The contour will look like a circle after scaling.
Problem: Is converge result which is scaled the same as converge result which is not scaled.
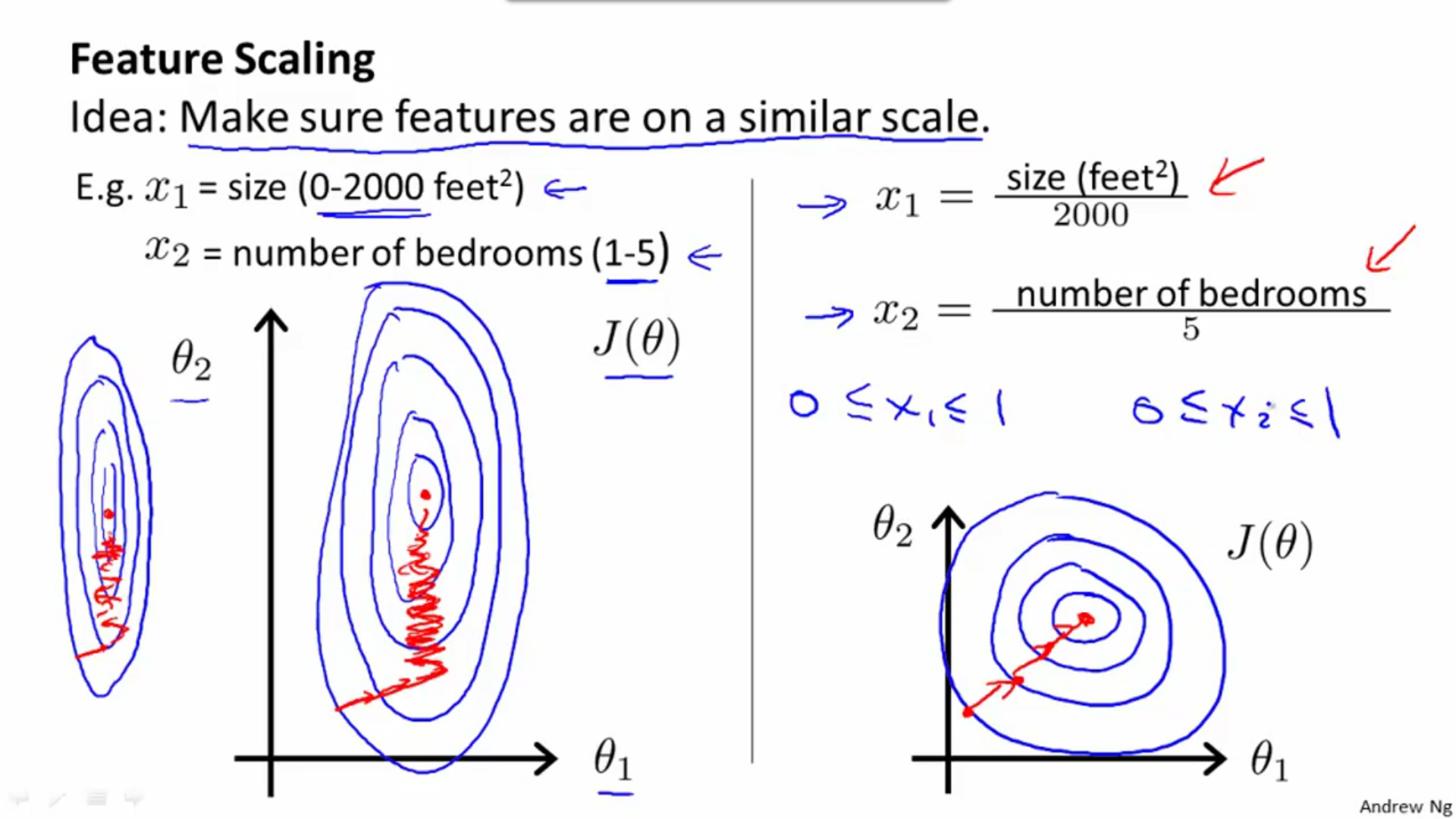
If scale of feature is similar to [-1,1], it will be fine. When it is too big or too small, it should be scaled.

Mean normalization:

Learning rate
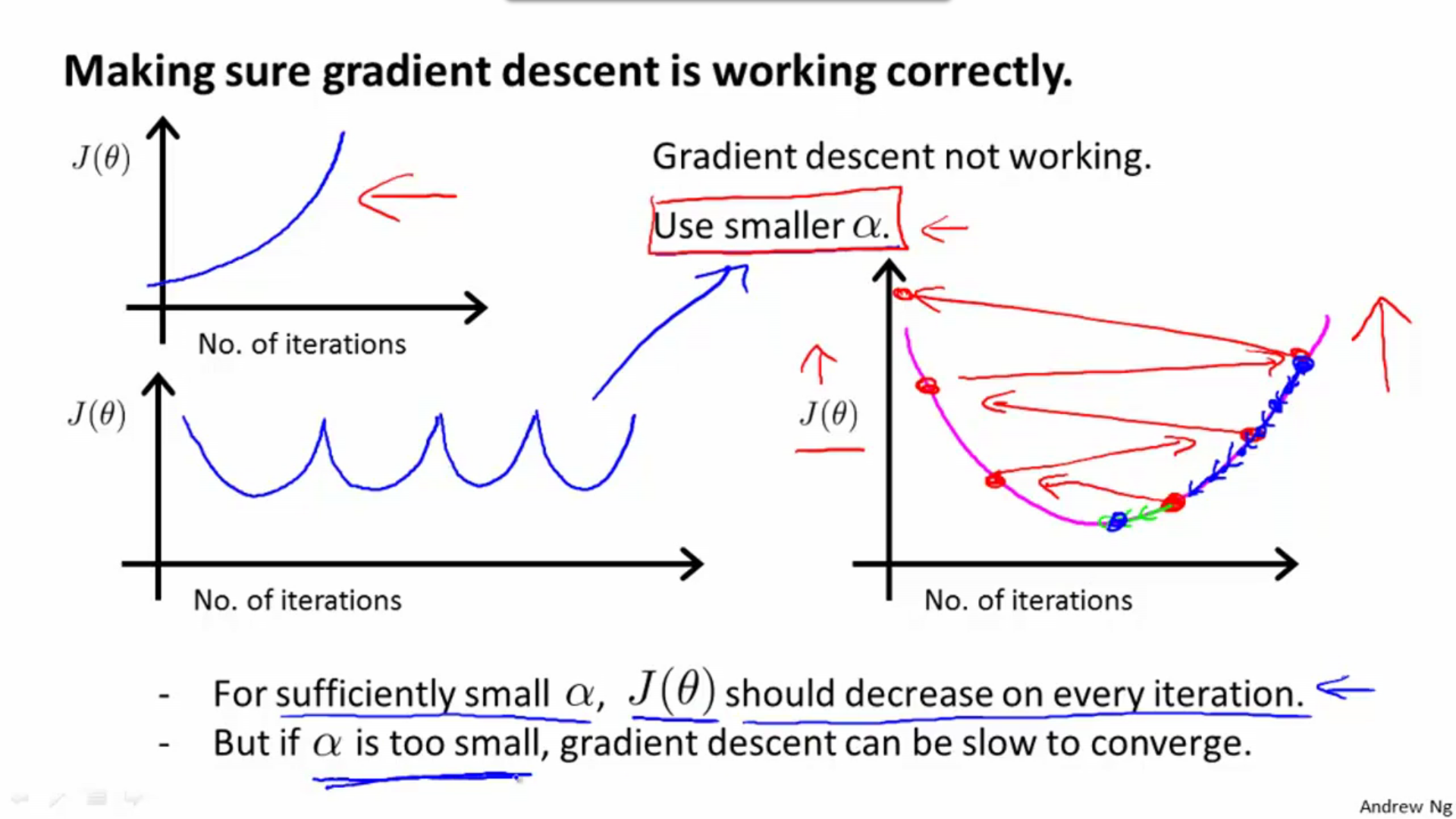
Check if gradient descent works correctly using this plot: min(J) - iteration number.

Alpha can’t be too small or too big, we can check it using descent rate plot.
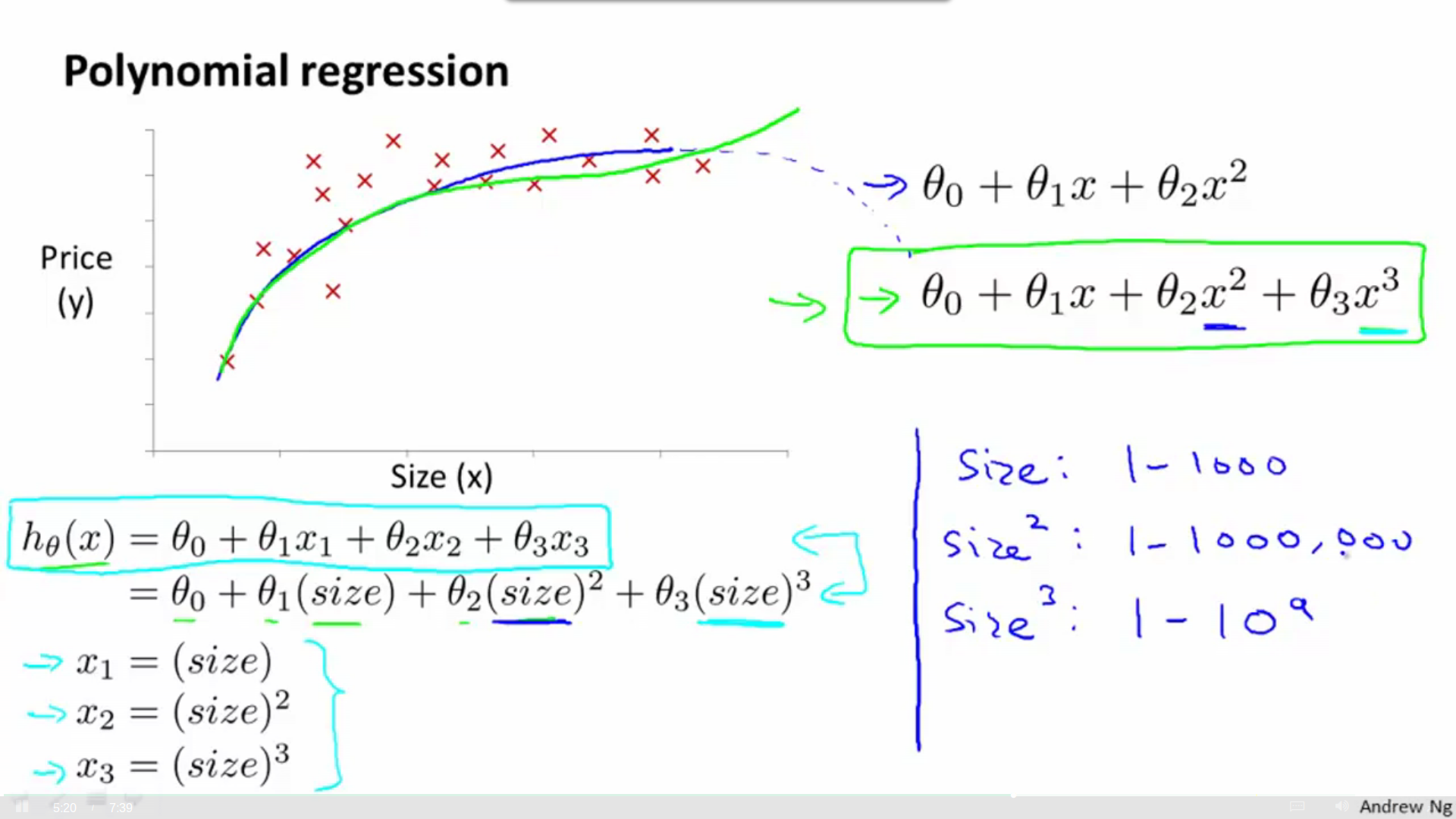
Polynomial regression
We can combine multiple features into one, or use polynomial function.
Convert it into linear regression, but range of variables may differ widely, so it need feature scaling.
Computing parameters analytically
Normal Equation
Solve the optimal theta analytically just by one go.
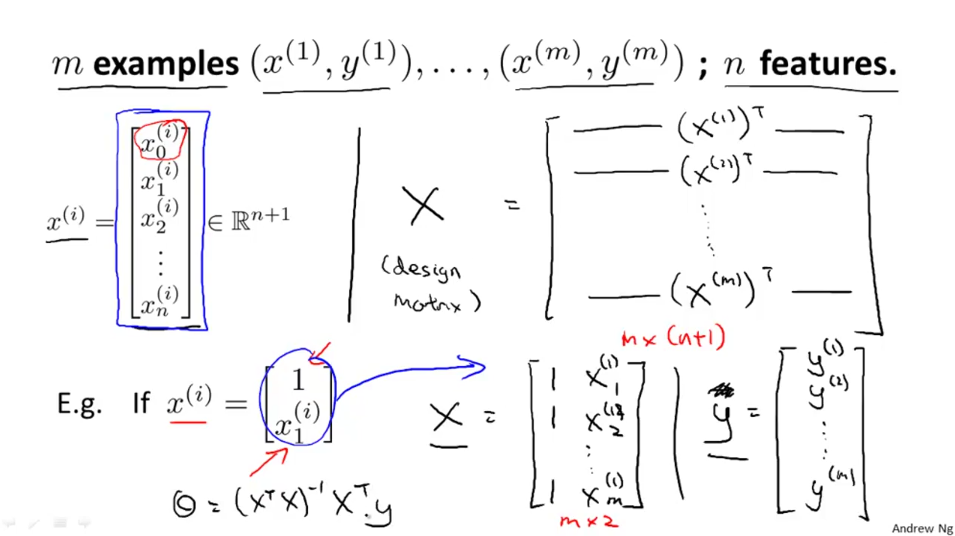
Matrix setup:
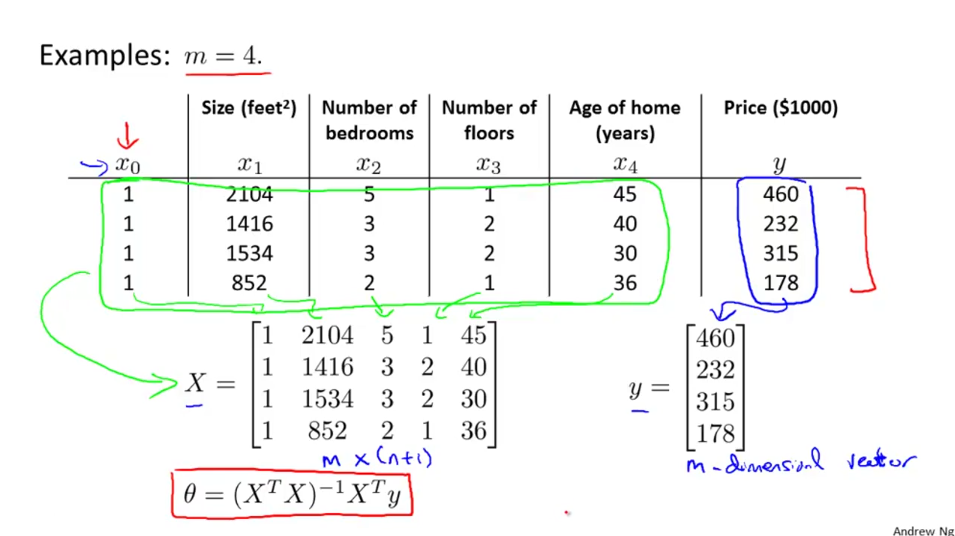
Derivation of theta: 知乎专栏
Normal equation don’t need feature scaling:
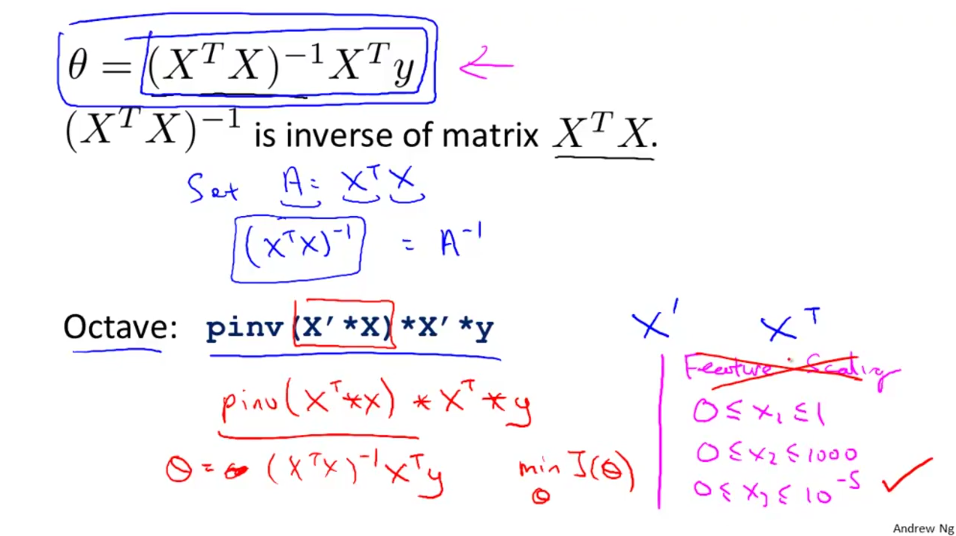
When number of features is small, normal equation is better. Otherwise, gradient descent is better.

What if X^T X is not invertable.
pinv() in octave will give a value even if parameter is not invertable; int() is not.

The reason why X^T X is not invertable:
1. Redundant feature;
2. Too many features.
